Questo articolo vuole essere un itinerario guidato attraverso la difficile materia della fisica stellare e dell'analisi spettrale, fino all'applicazione pratica di alcuni esperimenti per la verifica della teoria qui illustrata.

Non fatevi spaventare se lungo la strada incontrerete qualche formula un po' complessa: essa verrà comunque spiegata in termini semplici e vuole essere un approfondimento dei complicatissimi aspetti fisici del fantastico universo che ci circonda.

Il viaggio ci porterà dall'interno di una stella, dove avvengono le terrificanti reazioni nucleari che sono la vera "sorgente di vita" delle stelle stesse, fino alla sua superficie, dove gli scienziati riescono ad analizzarne gli aspetti grazie alla visione diretta e soprattutto alla spettrografia, che come vedremo ci permetterà di conoscere i più intimi aspetti di una stella e della materia che la compone, fino ad arrivare ad una vera e propria verifica sul campo di ciò che avremo illustrato qui.

Grazie infatti ad un esperimento con una semplice macchina fotografica ed un prisma, potremo vedere noi stessi gli spettri delle stelle e calcolare il diagramma di Hertzsprung e Russell, diagramma che è una dimostrazione grafico - visiva del "curriculum-vitae" di una stella, della sua età e delle sua caratteristiche fisiche.

Le stelle sono masse di gas le cui regioni centrali, soggette a una temperatura dell'ordine di milioni di gradi e a una pressione superiore a un miliardo di atmosfere, sono sede di reazioni nucleari dalle quali scaturisce l'energia irraggiata.

Sotto tali condizioni fisiche, molte sono le reazioni nucleari possibili: fu Bethe che, in seguito ad uno studio della vita media di tali reazioni, giunse alla conclusione che le reazioni che darebbero il maggior contributo energetico, sono quelle che portano alla formazione di nuclei di elio.

Sono due i principali processi che permettono la sintesi dell'elio dall'idrogeno: la reazione protone - protone (p-p) e il ciclo del carbonio - azoto (C-N), detto anche ciclo di Bethe - Weizsacker. Le reazioni fondamentali di tali processi portano a sostanziali modifiche degli atomi in gioco, con una notevole produzione di radiazioni di vario genere (luminosa, raggi gamma, ecc.). In particolare nella reazione protone – protone scompaiono 4 protoni su 6; si produce un nucleo di He⁴, 2 neutrini, 2 positroni che si annullano con 2e^- e radiazioni. In quella Carbonio – Azoto invece scompaiono 4 protoni, è prodotto un nucleo di He⁴, 2 positroni e radiazioni. Il carbonio C¹² ha in questo processo la funzione di semplice catalizzatore.

Le radiazioni che sono emesse in conseguenza dei suddetti processi, sono caratterizzate da cortissima lunghezza d'onda e vengono assorbite dalla materia stellare interna, costituita di plasma ad altissima temperatura e quindi opaco a tale radiazione. Tale plasma però riemette sotto altra forma l'energia assorbita (con lunghezza d'onda lambda maggiore) cosicché l'energia generata all'interno si trasmette da uno strato all'altro verso la superficie mantenendosi in quantità costante ma variando la lunghezza d'onda.

Nelle zone più esterne la radiazione è ricca soprattutto di radiazioni visibili, infrarosse e radioelettriche: questa zona esterna costituisce l'atmosfera stellare. L'analisi dell'irraggiamento stellare consente di determinare i parametri che caratterizzano l'atmosfera delle stelle, come temperatura, accelerazione di gravità, composizione chimica e i moti dell'atmosfera stellare.

La scoperta della fotografia segna l'inizio dello studio sistematico degli spettri stellari. Dal tempo della famosa esperienza di Newton si sa che la luce bianca può essere decomposta, con l'aiuto di un prisma. Nella spettrografia possono essere anche impiegati reticoli cioè lastre di vetro ottico su cui sono tracciate parecchie centinaia di solchi per millimetro, tutti paralleli fra loro. Mentre in uno spettrografo a prisma lo spettro viene prodotto dalla rifrazione del raggio luminoso all'interno del prisma, con i reticoli il fenomeno della diffusione dipende dalla lunghezza d'onda, e la loro applicazione è consigliabile solo per oggetti molto luminosi come il Sole.

La scomposizione dell'irraggiamento stellare ha luogo nello stesso modo, attraverso un prisma, in uno spettrografo collocato nel fuoco di un telescopio o direttamente davanti alla macchina fotografica. L'aspetto di uno spettro stellare, analogo a quello solare, presenta un fondo continuo brillante, solcato da righe scure dette righe di assorbimento.

Tramite esperienze di laboratorio si è potuto dimostrare che ogni atomo, quando è eccitato, emette radiazioni caratteristiche del suo elemento secondo la relazione

lambda = hc/E

dove lambda è la lunghezza d'onda della radiazione prodotta, E è l'energia liberata dal passaggio di un e- da uno stato quantico ad un altro, h è la costante di Planck, o quanto d'azione, h=6.6x10^-34 joule x sec, e c è la velocità della luce (c=299792 Km/sec).

Queste radiazioni costituiscono dunque un "messaggio" che ci permette di identificare la natura della sua sorgente, proprietà che è stata usata sin dagli inizi della spettroscopia stellare.

Le righe scure presenti sullo spettro stellare continuo furono scoperte per la prima volta da W.H.Wollaston nel 1802, nello spettro del sole. Ma la loro interpretazione fu possibile solo nel 1859, quando R.W.Bunsen e G.R. Kirchhoff stabilirono, in seguito alle loro ricerche di laboratorio, le leggi fondamentali dell'analisi spettrale, leggi dette appunto di Kirchhoff:

1. Un corpo incandescente, solido, liquido o gas ad alta pressione e temperatura, presenta uno spettro continuo di emissione, senza righe.
2. Un gas incandescente a bassa pressione presenta sullo spettro alcune luminose righe di emissione che gli sono caratteristiche, in modo da poter dedurre da esso la composizione chimica del gas in esame.
3. Se attraverso un gas si fa passare la luce emessa da un corpo che presenta uno spettro continuo, su di esso appaiono le righe caratteristiche del gas; se questo si trova ad una temperatura maggiore di quella della sorgente, le righe sono di emissione, più luminose dello sfondo continuo; se il gas si trova ad una temperatura minore, le righe sono di assorbimento, meno luminose del continuo.

Dunque, in base a queste leggi e a quanto detto prima riguardo all'atmosfera e struttura delle stelle, la fotosfera si comporta come sorgente caratterizzata da uno spettro continuo mentre gli strati sovrastanti o cromosfera, più fredda e a pressione minore, sono all'origine delle righe di assorbimento.

Con l'identificazione di tali righe è possibile effettuare un'analisi chimica qualitativa dell'atmosfera della stella. Più difficile si presenta un'analisi quantitativa, che permetta di determinare la percentuale dei diversi elementi atomici presenti. Infatti l'intensità di una riga di assorbimento non dipende solamente dal numero di atomi che la producono, ma anche da altri parametri, quali la temperatura, la pressione ecc., e poiché i valori di questi non sono disponibili con sufficiente precisione, le analisi quantitative risultano affette da un certo errore e sono effettuate raramente.

Anche le temperature superficiali delle stelle si possono rilevare dallo spettro: vale infatti la legge di Wien (1864-1928) o legge dello spostamento, per cui il massimo di intensità dello spettro continuo dipende dalla temperatura secondo la formula:

lambda max . T = 2.8978 m . °K

dove lambda max è la lunghezza d'onda del massimo d'intensità, espressa in Angstrom; tale legge vale esattamente solo per il cosiddetto CORPO NERO e cioè il corpo che assorbe completamente tutte le radiazioni che lo colpiscono e, viceversa, riscaldato, si comporta come perfettamente irradiante.

In realtà però le stelle non sono corpi neri perfetti e quindi la radiazione emessa a qualsiasi temperatura è sempre inferiore, per ogni lunghezza d'onda, a quella emessa dal corpo nero.

Volendo rappresentare graficamente la distribuzione spettrale dell'energia emessa da un corpo nero, possiamo servirci della legge di Planck (1858-1947) e il risultato mostra le ben note "planckiane", che presentano, in accordo con la legge dello spostamento di Wien, un massimo che si sposta, al diminuire della temperatura, verso lunghezze d'onda maggiori.

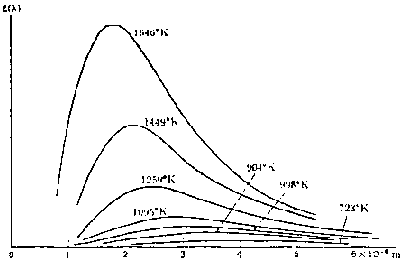
La temperatura ricavata viene detta temperatura fotosferica efficace ed è la temperatura che dovrebbe possedere un corpo nero di area uguale a quella della superficie stellare per irradiare lo stesso flusso di energia che, come si può ricavare dalla Figura 1, è l'area della planckiana corrispondente alla T fotosferica, ottenibile integrando la formula di Planck, rappresentante la curva, per tutte le lunghezze d'onda, da 0 a infinito:

L'analisi spettrale permette inoltre di ottenere informazioni circa il moto di una stella lungo la direzione che va dalla Terra alla stella stessa, cioè di conoscere la velocità radiale, in base all'effetto Doppler (1803-1853): infatti una sorgente di luce che si avvicini all'osservatore, ha il suo spettro spostato verso il violetto, mentre lo spostamento è verso il rosso in caso di allontanamento. Gli spostamenti per effetto Doppler sono più evidenti sulle righe spettrali; la velocità radiale è poi semplicemente ricavabile dalla relazione

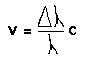
dove Delta lambda è lo spostamento della riga spettrale con lunghezza d'onda lambda, c è la velocità della luce. Se però le velocità in gioco si avvicinano a quelle della luce, bisogna impiegare una formula più generale prevista dalla teoria della relatività di Einstein.

Tale proprietà dello spettro elettromagnetico è applicata anche e soprattutto nello studio dei moti delle galassie, per un'ulteriore conoscenza dell'espansione dell'universo e della distribuzione della materia spaziale. Anche lo studio delle stelle doppie è aiutato dalla conoscenza dello spettro elettromagnetico. Molte doppie infatti non sono separabili otticamente, per la limitatezza dello strumento o per la turbolenza atmosferica, mentre lo sono spettroscopicamente.

Se la differenza di magnitudine delle due componenti è piccola, lo spettro presenterà 2 sistemi di righe distinti, oscillanti con lo stesso periodo: infatti nel corso del moto orbitale, una stella si approssima all'osservatore in un semiperiodo mentre l'altra se ne allontana: i due sistemi di righe dunque, per l'effetto Doppler, presenteranno spostamenti complementari - l'uno verso il rosso, l'altro verso il violetto - attorno ad un centro (una riga) comune, come mostra la Figura 2.

L'utilità nello studio degli spettri non finisce qui, anzi le applicazioni sono veramente innumerevoli. Degno di nota è lo studio dei campi magnetici stellari grazie all'effetto Zeeman (1865-1943) secondo cui se una sorgente luminosa si trova in un campo magnetico, le sue righe spettrali vengono a suddividersi in due o più componenti. Dall'entità della separazione è possibile dedurre l'intensità del campo magnetico. Se i raggi luminosi sono emessi perpendicolarmente al campo magnetico, si osserverà la formazione di un tripletto, cioè una separazione della riga originaria in 3 componenti, una nella posizione della riga originaria, le altre in posizione opposta e simmetrica (effetto Zeeman trasversale). Se i raggi luminosi sono invece paralleli alle linee di forza, si verifica la separazione in un doppietto. In realtà le separazioni possono essere anche molto più complesse e in più componenti, secondo leggi alquanto elaborate.

Per ultimo è da notare lo studio della materia interstellare grazie a particolari righe di assorbimento che appaiono su alcuni spettri stellari. Si notano infatti righe molto sottili di calcio ionizzato e di sodio neutro, la cui velocità radiale differisce da quella delle altre righe dello spettro. Questo fenomeno si spiega ammettendo che queste righe non si formino nell'atmosfera della stella, ma nello spazio situato tra la stella e l'osservatore. Altre righe sono state scoperte dal momento delle prime osservazioni, dovute al potassio, al ferro, alle molecole di CH (idruro di carbonio) ecc., che riflettono la componente gassosa della materia interstellare, con densità media di un decimo di atomo per cm³ e con punte massime di 100 atomi per cm³.

Passando attraverso l'atmosfera terrestre, l'irraggiamento proveniente dagli astri subisce una degradazione assai severa. L'intera regione ultravioletta (con lambda < 5000 Angstrom) è assorbita completamente dall'ozono atmosferico, mentre con lambda abbastanza grande, nell'infrarosso, l'ossigeno e il vapor acqueo perturbano seriamente gli spettri. Nella finestra radio l'atmosfera ridiventa trasparente e l'osservazione è ancora possibile. I telescopi collocati su satelliti artificiali (Hubble, HST) costituiscono quindi una nuova tappa dell'astrofisica, ampliando il campo dello studio degli spettri e di tutte le conoscenze da esso derivanti.

Un'analisi sommaria degli spettri stellari rivela che essi presentano una grande varietà. Sono costituiti tutti da un fondo continuo brillante solcato da righe di assorbimento e, eccezionalmente, da righe di emissione; ma la ripartizione dell'intensità del fondo continuo e la posizione di queste righe non sono le stesse per tutti gli spettri.

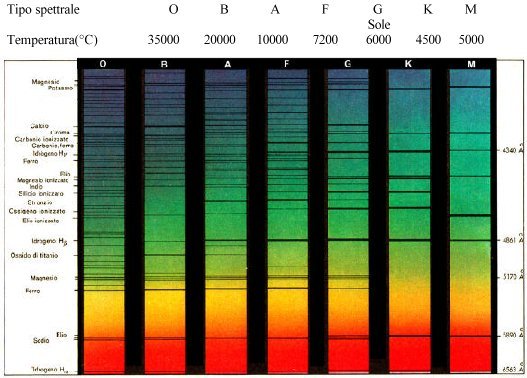
Sin dall'inizio della spettroscopia stellare è stata sentita l'esigenza di classificare le stelle secondo l'apparenza degli spettri. L'attuale classificazione fu fissata intorno al 1900 all'osservatorio di Harvard da Pickering e dai suoi collaboratori; essi dimostrarono che la maggior parte (99%) delle stelle poteva essere classificata secondo una sequenza continua di tipi spettrali, designati dalle lettere maiuscole: O, B A, F, G, K, M, R, N, S.

Per precisare questa classificazione, si fu indotti a suddividere ogni tipo in 10 sottoclassi rappresentate ciascuna da un numero da 0 a 9, fatto seguire dalla lettera che indica il tipo spettrale. Il passaggio dal tipo B al tipo A, per esempio, avrà luogo attraverso la sequenza B0, B1, B2, ... B8, B9, A0, A1 ...

Gli spettri che non rientrano nel quadro di questa sequenza furono indicati con dei suffissi come "n", per righe larghe e diffuse, "s" per righe sottili, "e" per la presenza di righe di emissione, "p" per particolarità diverse dalle precedenti.

L'importanza della classificazione spettrale delle stelle sta principalmente nel fatto che essa è strettamente connessa alla principale caratteristica fisica delle stelle, la loro temperatura. La linearità e la continuità della sequenza spettrale infatti, indicano che lo stato fisico dell'atmosfera delle stelle presenta una variazione continua in funzione di un parametro principale, la temperatura appunto.

Infatti le caratteristiche delle successive classi spettrali sono sufficienti per comprendere che le loro differenze sono essenzialmente imputabili ad una variazione continua di eccitazione degli atomi esistenti nell'atmosfera delle stelle e che il grado di eccitazione va regolarmente decrescendo lungo la sequenza dai tipi O, B verso i tipi K, M.

Questo fatto, unito al regolare mutamento di colore dall'azzurro al rosso, indica con assoluta certezza che la successione spettrale delle stelle è un ordinamento per temperature decrescenti delle fotosfere e atmosfere stellari.

Così, se gli spettri delle cosiddette "stelle a idrogeno" presentano le righe dell'H molto intense, non significa necessariamente che queste stelle siano più ricche di H di altre, bensì che per la loro diversa temperatura, la materia stellare delle prime è diversamente eccitata delle altre.

Contrariamente a quello che potrebbe sembrare, fotografare uno spettro stellare non e poi così difficile. Lo spettrografo di cui ci si può servire è semplicemente costituito da una macchina fotografica, con montato un teleobiettivo 200 mm, davanti al quale è posto un normalissimo prisma montato su un supporto metallico: La Figura 4 può mostrare più chiaramente questa semplice apparecchiatura

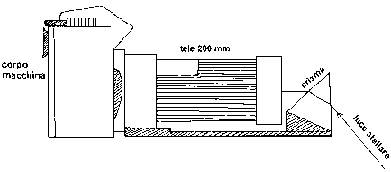
che è una versione semplificata dello spettrografo cosiddetto a "prisma obiettivo", normalmente usato negli osservatori astronomici, che è schematizzato in Figura 5.

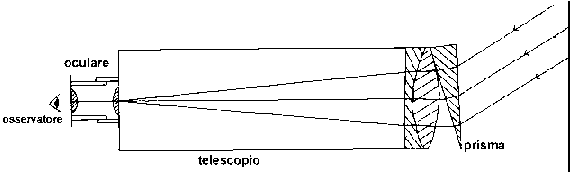
L'uso di un tele 200mm si rende necessario per ottenere immagini abbastanza ingrandite, tali da non dover essere ingrandite troppo nella successiva fase di stampa.

Il puntamento di una stella avviene inclinando la macchina di un certo angolo rispetto alla direzione verso cui punta l'obiettivo, data la deviazione che i raggi luminosi subiscono nel passare attraverso il prisma; è preferibile inoltre che la stella sia più alta possibile sull'orizzonte, riducendo così notevolmente gli effetti di turbolenza atmosferica (seeing).

La posa di alcuni minuti è resa necessaria per la debolezza della luminosità dello spettro, dovuta alla dispersione del prisma e al rapporto focale del teleobiettivo usato. In ogni caso il moto stellare durante la posa provoca un movimento lineare sulla pellicola che permette di aumentare l'ampiezza dello spettro (che altrimenti risulterebbe una sottile striscia verticale) migliorando cosi l'aspetto generale della fotografia.

Le 3 fotografie presentate (Figure 6a, 6b, 6c) mostrano rispettivamente gli spettri di Rigel (Beta Orionis), di Vega (Alpha Lyrae) e di Betelgeuse (Alpha Orionis), ottenuti con lo spettrografo sopra descritto. Queste stelle appartengono rispettivamente alle classi spettrali B8, A0,M0.

La forma a parallelogramma è stata causata, come detto in precedenza, dal moto stellare durante la posa, data la difficoltà di un perfetto puntamento e allineamento del prisma con le traiettorie stellari. È interessante notare, nonostante la semplice apparecchiatura usata, quali caratteristiche appaiono sui 3 spettri. Innanzitutto gli spettri di Rigel e di Vega sono molto ricchi di radiazioni azzurre, caratteristica questa di stelle ad alta temperatura (T>10⁴ °C), mentre nello spettro di Betelgeuse (T = 3x10³ °C circa) c'è scarsa presenza di tale radiazione. Inoltre si può notare come nello spettro di Vega sono evidenti le righe di assorbimento dovute all'idrogeno (serie di Balmer), mentre in quello di Betelgeuse, proprio a causa della temperatura relativamente bassa, sono presenti bande molecolari di assorbimento dovute principalmente all'ossido di titanio nel verde attorno ai 4900 A.

L 'esperienza è comunque risultata più che significativa considerando il semplicissimo strumento usato e permette, in ogni caso, di riconoscere i principali tipi spettrali di stelle, verificando la teoria degli spettri elettromagnetici enunciata nei primi paragrafi.

Grande importanza per lo studio di tutti i problemi dell'astronomia stellare, in particolare per quello dell'evoluzione stellare, ha assunto negli ultimi decenni il diagramma scoperto empiricamente attorno al 1910 da Ejnar Hertzsprung, danese, ed Henry Norris Russell, americano, indipendentemente l'uno dall'altro, il quale mette in relazione la luminosità intrinseca delle stelle e il loro tipo spettrale. A tale grafico, ogni punto del quale rappresenta una stella, è stato dato il nome di diagramma di Hertzsprung e Russell, o più brevemente, diagramma di H-R.

Fu Russell che per primo ottenne uno di questi diagrammi, riportando la luminosità assoluta di un certo numero di stelle (le più vicine a noi, delle quali conosceva le parallassi, e quindi le distanze) in funzione della loro classe spettrale. In Figura 7 si può vedere tale diagramma:

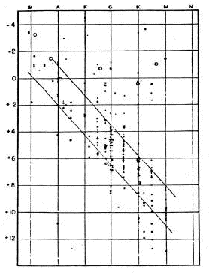
Gli stessi risultati erano stati ottenuti contemporaneamente da Hertzsprung, che aveva però considerato solamente luminosità apparenti di stelle in alcuni ammassi stellari aperti come le Pleiadi e le Iadi.

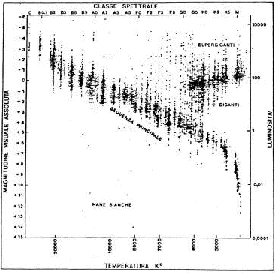
La forma più moderna e arricchita di un maggior numero di stelle permette di fare un'analisi più dettagliata di tale diagramma.

Nella Figura 8, il grafico mostra in ascisa la temperatura superficiale delle stelle e, parallelamente, la loro classificazione spettrale secondo Harvard; ciò è possibile, perché è dimostrato che le stelle appartenenti ad una certa classe spettrale sono caratterizzate da una ben determinata temperatura e così viceversa. Sull'asse delle ascisse potrebbe poi trovare posto una terza grandezza e cioè l'indice di colore delle stelle.

Infatti per due stelle aventi magnitudini apparenti rispettivamente m1 e m2, la formula di Pogson ci dice che la differenza di magnitudine fra le due stelle è data da

m 1 - m 2 = -2.5 log [I 1 (lambda) / I 2 (lambda)],

dove I1(lambda) e I2(lambda) stanno ad indicare gli illuminamenti dati dalle due stelle, relativamente ad una certa lunghezza d'onda. Se si considera ora una sola stella e si analizza la sua radiazione luminosa a due diverse lunghezze d'onda, fotografando la stella con due filtri diversi, uno blu per avere la magnitudine fotografica e uno giallo per quella visuale, la radiazione luminosa incidente sulla pellicola è caratterizzata da lunghezze d'onda diverse, che chiameremo lambdapg nel caso di uso del filtro blu e lambdav, nel caso si utilizzi il filtro giallo. La differenza fra la magnitudine fotografica e quella visuale così ricavate viene detta indice di colore detto C.I. (Colour Index) e, secondo la formula di Pogson è data da

C.I. = m pg - m v = -2.5 log [I 1 (lambda pg) / I 2 (lambda v)],

dove ora I(lambda pg) e I(lambda v) sono gli illuminamenti relativi a 2 distinte lunghezze d'onda.

Da queste considerazioni deriva che l'indice di colore dipende solo dal rapporto fra la quantità di energia emessa in due diverse regioni dello spettro di una stella, rapporto che, come è stato detto, è funzione della sola temperatura.

L'indice di colore assume per convenzione il valore zero per le stelle bianche di tipo A0 è negativo per le stelle più azzurre e positivo per le più rossastre. Tale sostituzione delle classi spettrali con l'indice di colore è molto utile e soprattutto più precisa per ricavare le temperature delle stelle più deboli, meno sensibili ad un'analisi spettroscopica.

Riprendendo il discorso sul diagramma H-R, in Figura 8 in ordinata troviamo la magnitudine visuale assoluta e la luminosità riferita al sole parallelamente. Si può ben notare la non casualità della distribuzione dei punti rappresentativi delle stelle nel grafico. Vi è infatti una fascia diagonale detta serie o sequenza principale, che contiene un gran numero di stelle, la luminosità delle quali diminuisce col diminuire della loro temperatura: è la sequenza delle cosiddette nane normali. Un'altra zona in alto a destra del diagramma è abbastanza affollata di stelle: è la fascia delle giganti rosse, con luminosità molto simili fra loro anche se di temperature abbastanza diverse. Altra zona di raggruppamento, anche se minore, si trova in basso a sinistra, in cui si trovano le nane bianche, poco luminose ma con temperature elevate.

Gli appellativi assegnati a queste stelle (nane e giganti) sono dovuti al fatto che Russell, nelle sue osservazioni notò che stelle appartenenti a stesse classi spettrali, quindi con circa la stessa temperatura, mostravano una maggiore o minore luminosità. Essendo la temperatura la stessa, egli ne dedusse che questa differenza di luminosità non poteva che essere dovuta ad una diversa superficie radiante, ovvero ad un diverso raggio delle stelle, perché la luminosità delle stelle è proporzionale alla superficie raggiante 4 . pigreco . R² ed a T⁴.